

14.3.2频率分布直方图
一、单选题
1.为了解学生在“弘扬传统文化,品读经典文学”月的阅读情况,现从全校学生中随机抽取了部分学生,并统计了他们的阅读时间(阅读时间),分组整理数据得到如图所示的频率分布直方图.则图中a的值为()
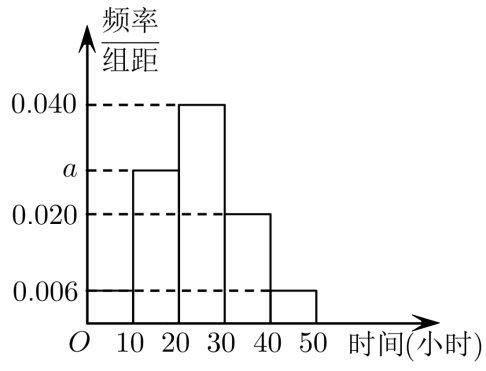
A.0.028B.0.029C.0.280D.0.290
【答案】A
【解析】
【分析】
由频率之和等于得出
的值.
【详解】
由得
.
故选:A
2.某购物广场开展的“买三免一”促销活动异常火爆,对其中一日8时至22时的销售额进行统计,组距为2小时的频率分布直方图如图所示.已知12时至l6时的销售额为90万元,则10时至12时的销售额为().
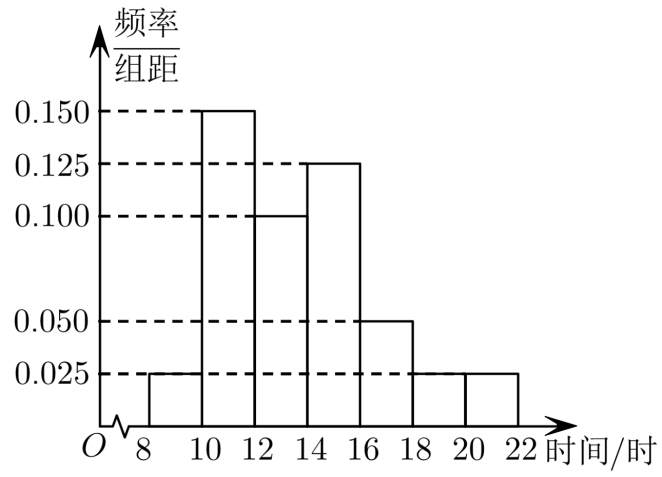
A.60万元B.80万元C.100万元D.120万元
【答案】A
【解析】
【分析】
依据频率分布直方图的性质即可求得10时至12时的销售额.
【详解】
12时至l6时的频率为,10时至12时的频率为
10时至12时的销售额![]() (万元)
(万元)
则故选:A
3.从某中学随机抽取100名学生,将他们的身高数据(单位cm)绘制成频率分布直方图,若要从身高在三组内的学生中,用分层抽样的方法选取16人参加一次活动.则从身高在
内的学生中选取的人数应为()
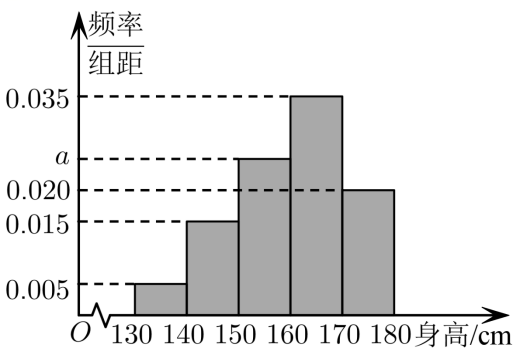
A.3B.4C.5D.7
【答案】B
【解析】
【分析】
先求得的值,然后结合分层抽样的知识计算出正确答案.
【详解】
依题意,解得
,
身高在三组内的学生比例为
,
用分层抽样的方法选取16人参加一次活动,
则从身高在内的学生中选取的人数应为
人
故选:B
4.下列说法不正确的是()
A.频率分布直方图中每个小矩形的高就是该组的频率
B.频率分布直方图中各个小矩形的面积之和等于1
C.频率分布直方图中各个小矩形的宽一样大
D.频数分布直方图中每个长方形的高就是该组的频数
【答案】A
【解析】
【分析】
根据频率分布直方图和频数分布直方图的性质和特点即可判断四个选项的对错.
【详解】
解:对于,频率分布直方图中每个小矩形的高是该组的频率与组距的比值,故A错误;
对于,频率分布直方图中各个小矩形的面积之和等于1,是频率和为1,故B正确;
对于,频率分布直方图中各个小矩形的宽是组距,一样大,故C正确;
对于正确.
故选:A.
5.某中学统计了初中毕业班一次模拟考试后学生的数学成绩,所得频率分布直方图结束如图所示,若已知的学生的数学成绩不大于
分,则
的估计值为()

A.B.
C.
D.
【答案】A
【解析】
【分析】
根据频率分布直方图可得出关于实数的等式,解出实数
的值,即为所求.
【详解】
由频率分布直方图知,解得
.
前三组的频率之和为
,
而前四组的频率之和为,
由
,解得
,即
的估计值为
.
故选:A.
【点睛】
方法点睛:从频率分布直方图中得出相关数据的方法
(1)频率:频率分布直方图中横轴表示样本数据,纵轴表示![]() ,即每个小长方形的面积表示相应各组的频率.
,即每个小长方形的面积表示相应各组的频率.
(2)众数:频率分布直方图中最高的小长方形底边中点对应的横坐标.
(3)中位数:平分频率分布直方图中小长方形的面积且垂直于横轴的直线与横轴交点的横坐标.
(4)平均数:频率分布直方图中每个小长方形的面积与对应小长方形底边中点的横坐标的乘积之和.
6.为了解学生在“弘扬传统文化,品读经典文学”月的阅读情况,现从全校学生中随机抽取了部分学生,并统计了他们的阅读时间(阅读时间),分组整理数据得到如图所示的频率分布直方图.则图中a的值为()
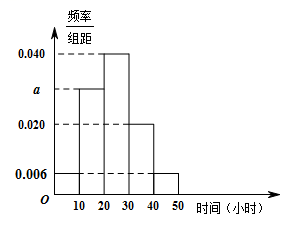
A.0.028B.0.030C.0.280D.0.300
【答案】A
【解析】
根据五个矩形的面积和为1列式可得结果.
【详解】
由得
.
故选:A
二、多选题
7.(多选)如图给出的是某高校土木工程系大四55名学生期末考试专业成绩的频率折线图,其中组距为10,且本次考试中最低分为50分,最高分为100分.根据图中所提供的信息,下列结论中正确的是()
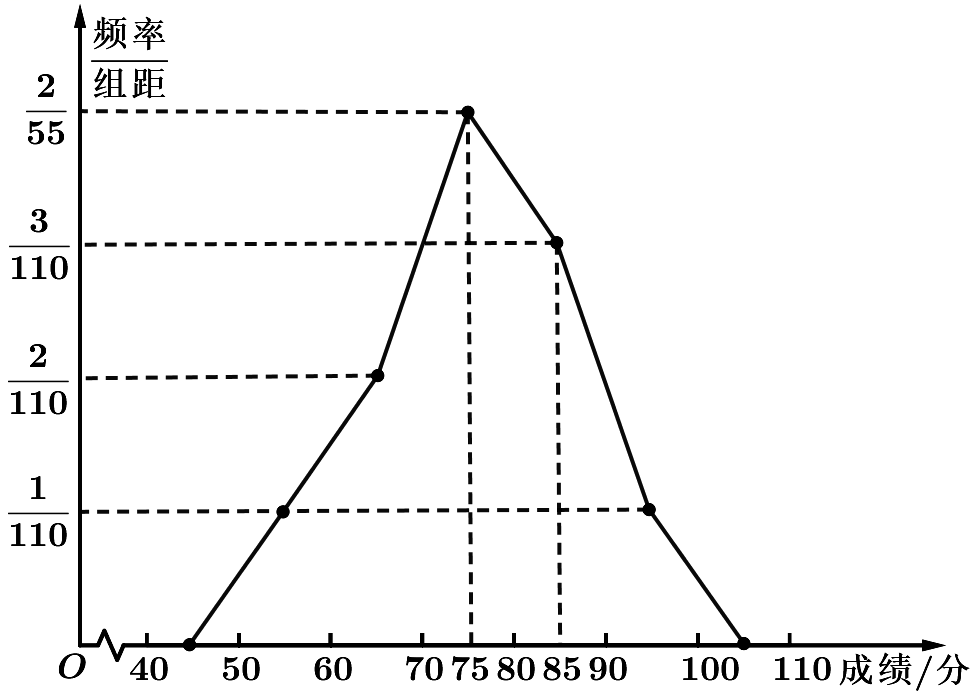
A.成绩是75分的人数为20
B.成绩是100分的人数比成绩是50分的人数多
C.成绩落在内的人数为35
D.成绩落在内的人数为20
【答案】CD
【解析】
【分析】
根据折线图提供的数据及概率的意义判断各选项.
【详解】
成绩落在内的人数为
![]() ,不能说成绩是75分的人数为20,所以A错误,D正确;
,不能说成绩是75分的人数为20,所以A错误,D正确;
从频率折线图看不出成绩是100分的人数比成绩是50分的人数多,只能看出成绩落在内的人数和成绩落在
内的人数相等,所以B错误;
成绩落在内的人数为
![]() ,所以C正确.
,所以C正确.
故选:CD.
8.(多选)学校为了解新课程标准中提升阅读要求对学生阅读兴趣的影响情况,随机抽取100名学生进行调查.根据调查结果绘制学生周末阅读时间的频率分布直方图如图所示.将阅读时间不低于的学生称为阅读霸,则下列结果正确的是()
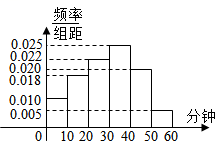
A.抽样表明,该校约有一半学生为阅读霸
B.抽取的100名学生中有50名学生为阅读霸
C.该校学生中有50名学生不是阅读霸
D.抽样表明,该校有50名学生为阅读霸
【答案】AB
【解析】
根据频率分布直方图的数据列出频数分布表,从样本估计总体,得出结果.
【详解】
根据频率分布直方图可列下表:
阅读时间/min
抽样人数/名
10
18
22
25
20
5
抽取的100名学生中有50名为阅读霸,据此可判断该校约有一半学生为阅读霸.
故选:AB
【点睛】
本题主要考查频率分布直方图的应用和由样本数据估计总体,属于基础题.
三、填空题
9.中小学生的视力状况受到社会的关注.某市有关部门从全市6万名高一学生中随机抽取400名学生,对他们的视力状况进行一次调查统计,将所得到的有关数据绘制成频率分布直方图,如图所示,从左至右五个小组的频率之比为,则抽取的这400名高一学生中视力在
范围内的学生有______人.
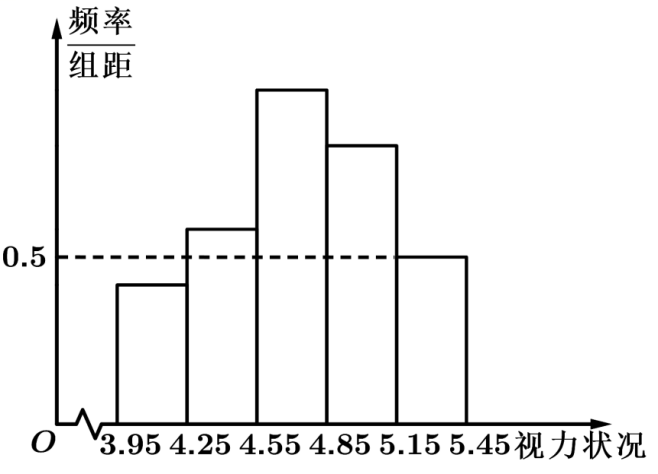
【答案】50
【解析】
【分析】
利用频率分布直方图的性质求解即可.
【详解】
第五组的频率为,
第一组所占的频率为![]() ,
,
则随机抽取400名学生视力在范围内的学生约有
人.
故答案为:50.
10.为了解某校高三学生联考的数学成绩情况,从该校参加联考学生的数学成绩中抽取一个样本,并分成五组,绘成如图所示的频率分布直方图.已知第一组至第五组的频率之比为,第五组的频数为6,则样本容量为______.
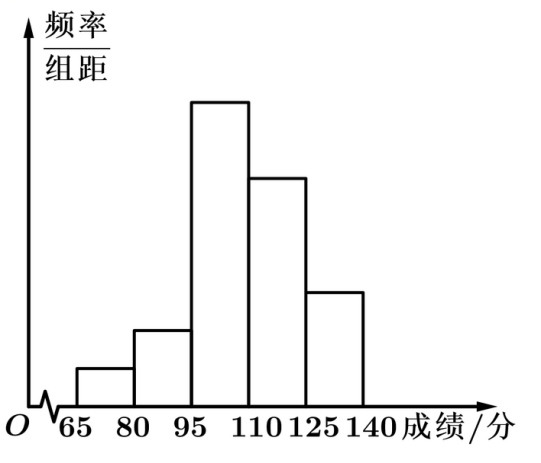
【答案】40
【解析】
【分析】
根据频率直方图及题中数据,计算第五组的频率,再结合第五组的频数求解样本容量即可.
【详解】
因为第一组至第五组的频率之比为,
可设第一组至第五组的频率分别为,又频率之和为1,
所以,解得
![]() ,
,
第五组的频率为,又第五组的频数为6,
所以样本容量为![]() .
.
故答案为:40.
11.一组数据的频率直方图中,所有小长方形的面积总和为________.
【答案】1
【解析】
【分析】
由频率分布直方图的性质求所有小长方形的面积.
【详解】
一组数据的频率直方图中,所有小长方形的面积总和为1.
故答案为:1
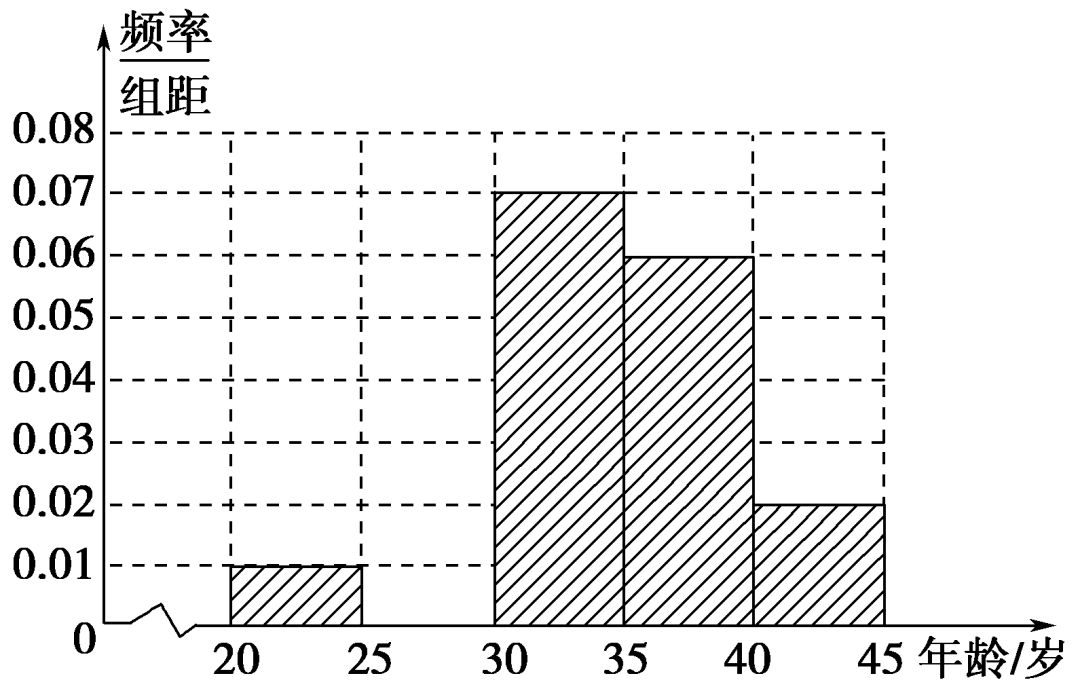
12.对某项活动中800名志愿者的年龄抽样统计后,得到如图所示的频率分布直方图,但是年龄在[25,30)内的数据不慎丢失,依据此图可得.年龄在[25,30)内对应小长方形的高度为________.
【答案】0.04
【解析】
【分析】
设设年龄在[25,30)内对应小长方形的高度为x,根据频率分布直方图中所有小长方形的面积和等于1列出方程,解方程即可.
【详解】
设年龄在[25,30)内对应小长方形的高度为x,则有5×(0.01+x+0.07+0.06+0.02)=1,解得x=0.04,所以年龄在[25,30)内对应小长方形高度为0.04.
故答案为:0.04.
13.根据某水文观测点的历史统计数据,得到某条河流水位的频率分布直方图(如图)从图中可以看出,该水文观测点平均至少一百年才遇到一次的洪水的最低水位是______米.
【答案】50
【解析】
【分析】
运用频率分布直方图的知识,可得到在水位处于这一组的频率为
,按照图表可判断平均至少一百年才遇到一次的洪水的最低水位.
【详解】
至少100年才遇到一次的的水位出现的频率小于,由频率分布直方图可知,在水位处于
这一组的频率为
而,则范围在
的洪水100年内平均可发生一次,按照图表可知,平均至少一百年才遇到一次的洪水的最低水位是50米
故答案为:50
14.在样本的频率分布直方图中共有个小矩形,若中间一个小矩形的面积等于其余
个小矩形面积的
,且样本容量为3200,则中间一组的频数为__________.
【答案】400.
【解析】
【分析】
根据中间一个小矩形的面积等于其余(n﹣1)个小矩形面积之和的,设出中间一个小矩形的面积是x,则其余(n﹣1)个小矩形面积之和为7x,得到中间一个的频率的值,用概率乘以样本容量得到结果.
【详解】
∵在样本的频率分布直方图中共有n个小矩形,
中间一个小矩形的面积等于其余(n﹣1)个小矩形面积之和的,
设中间一个小矩形的面积是x,则其余(n﹣1)个小矩形面积之和为7x,
∵x+7x=1,
∴x
∵样本容量为3200,
∴中间一组的频数是3200400,
故答案为:400.
【点睛】
本题考查频率分布表,考查频率分步直方图小正方形的面积等于这组数据的频率,注意小正方形的面积之间的关系不要弄混,本题是一个基础题.
其他精品教学资源请访问师梦圆官方网站:www.shimengyuan.com
点击下方“阅读原文”获取更多精品教学资源
